What You Didn’t Learn in Berkeley CS 188 — Part 1

Why isn’t there model-free policy iteration?

Berkeley’s CS 188 covers many important foundations of reinforcement learning. But there’s still a gap between what’s taught in that undergraduate course and the baseline expected if you’re working in the field.

Berkeley’s course covers, in no particular order:

• Basic search algorithms

• Constraint satisfaction problems (CSPs)

• Minimax (with alpha-beta pruning)

• Bayes nets

• Markov Decision Process (MDP) definition

• Policy iteration

• Q-learning (and some variations)

This material is foundational, but the way it’s taught often feels fragmented. My goal here is to reorganize the basics into a clearer ontology that naturally sets up modern, continuous-control methods. The information hierarchy, I’d argue, could be sharper than what’s presented in CS 188.

CS 188 Recap: Markov Decision Process Definition

If you already remember the basics from 188, you can skip this section. Reinforcement learning is typically formalized as a Markov Decision Process (MDP). The MDP specifies the environment:

• States S: possible configurations of the world.

• Actions A: moves the agent can take.

• Transitions P(s’ | s, a): probability of landing in s’ after taking action a in s.

• Rewards R(s, a, s’): immediate payoff for (s, a) → s’.

• Discount γ ∈ [0, 1): how much you value the future.

Those five define the problem itself. On the agent side, we define constructs that depend on the MDP:

• Policy π: a mapping from states to actions.

• Value function V^π(s): expected discounted return from state s under π.

• Q-function Q^π(s, a): expected return from (s, a) under π. If no π is present, then Q refers to the Q-values estimates that we have established so far.

A Clearer Ontology

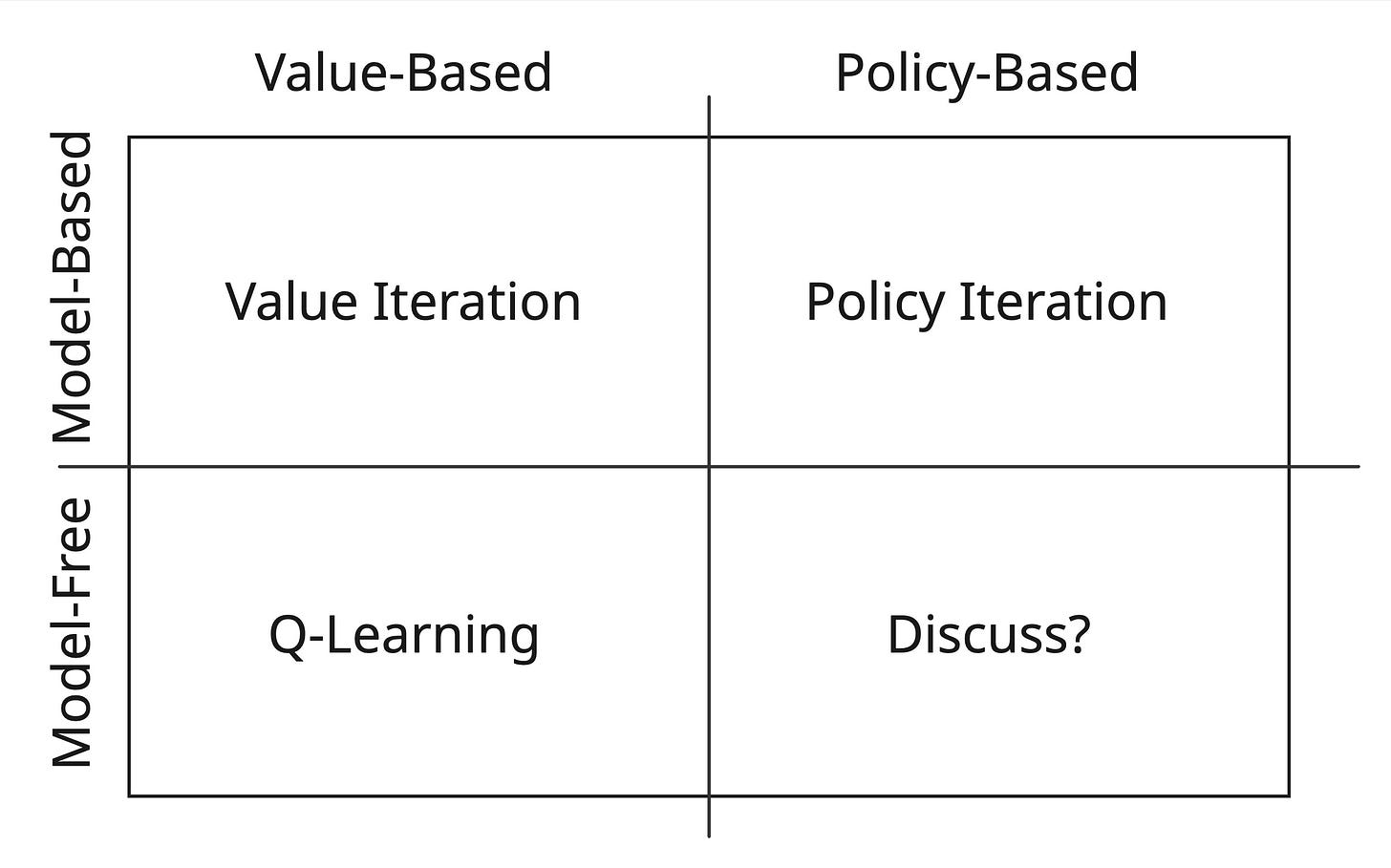
CS 188 distinguishes “model-based” vs. “model-free” methods:

• Model-based: assumes access to the transition probabilities and rewards (P and R).

• Model-free: learns from sampled experience without ever observing P or R directly.

Another useful axis is “policy-based” vs. “value-based”:

• Policy-based: directly solve for the optimal policy, then improve the value estimates by following that policy, repeating until convergence. (Many methods also use value estimates as baselines or for other purposes, e.g. actor-critic.)

• Value-based: solve V or Q directly until convergence, using the greedy policy that maximizes the expected value of the next state:

\(\pi(s) := \arg\max_a Q(s,a) = \sum_{s’} P(s’ \mid s,a) *\big(R(s,a,s’) + \gamma V(s’)\big)\)

So we have two orthogonal axes: model-based vs. model-free, and value-based vs. policy-based. Together they give us a 2-by-2 view of classical RL methods:

This is the ontology I propose. The last quadrant, model-free policy iteration, is the most interesting, and we’ll work our way toward it.

Value Iteration

Value iteration iteratively updates the value function until convergence. When you know P and R, the “Bellman optimality update” is:

\(V(s) \leftarrow \max_a \sum_{s’} P(s’ \mid s,a) * \big(R(s,a,s’) + \gamma V(s’)\big)\)

In other words, the value of a state is the maximum expected reward + discounted value of the next state. It’s implicitly summing an infinite discounted series. If V* is the fixed point of the update operator above, then:

\(V^*(s) = \mathbb{E}[R(s,a,s')] + \gamma \mathbb{E}[R(s', a', s’')] + \gamma^2 \mathbb{E}[R(s'', a’'s''')] + \cdots\)

Bellman Operator and Contraction

It makes sense that if we can solve for the fixed point V*, then we can define the optimal policy by greedily following whichever action maximizes the expected value of the next state. But how do we prove that the iterative process above actually converges?

To do so, we define the “Bellman optimality operator” (T) - the new value function if you perform a single iteration above:

\((TV)(s) = \max_a \sum_{s'} P(s' \mid s,a) * \big(R(s,a,s') + \gamma V(s')\big).\)

Then for any two value functions V and W:

\(\begin{align*} |(TV)(s) - (TW)(s)| &= \Big| \max_{a} \mathbb{E}_{s'}[R(s,a,s') + \gamma V(s')] - \max_{a} \mathbb{E}_{s'}[R(s,a,s') + \gamma W(s')] \Big| \\ &\leq \max_{a} \Big| \mathbb{E}_{s'}[R(s,a,s') + \gamma V(s')] - \mathbb{E}_{s'}[R(s,a,s') + \gamma W(s')] \Big| \\ &= \max_{a} \Big| \mathbb{E}_{s'}[\gamma (V(s') - W(s'))] \Big| \\ &\leq \gamma \max_{a} \mathbb{E}_{s'}\big[|V(s') - W(s')|\big] \\ &\leq \gamma \max_{s'} |V(s') - W(s')| \\ &= \gamma \, \|V - W\|_\infty. \end{align*}\)

And since we didn’t specify which s:

\(\quad \|TV - TW\|_\infty \;\leq\; \gamma \, \|V - W\|_\infty.\)

where that infinity operator refers to the maximum distance between any two states. In other words, when you apply the Bellman update operator to any two value functions, the resulting value functions are closer together.

That matters because you can now show that T must converge to a single fixed point. The proof is simple. Assume that there are two possible fixed points. Then the update above moves them closer together, meaning that there cannot be any non-zero distance between the points. To show existence, we need to know that if you keep getting closer and closer to some limit, then that limit is still a valid value function. For finite state spaces this is obvious because value functions are just real vectors, and in Rⁿ every Cauchy sequence converges. This is called the “Banach fixed point theorem”.

Iterative Expansion

Notice that after one application:

\(TV(s) = \mathbb{E}_{s’}[R(s,a_1,s’)] + \gamma \mathbb{E}_{s’}[V(s’)]\)

where a₁ is the action recommended by the greedy policy given V. After two iterations:

\(T^2V(s) = \mathbb{E}_{s''}[R(s,a_2,s'')] + \gamma \mathbb{E}_{s'}[R(s,a_1,s')] + \gamma^2 \mathbb{E}_{s'}[V(s')]\)

Each step adds one more discounted term. Early actions can be wrong, but their contribution shrinks geometrically. Eventually you converge to V*. In practice, you can truncate after k terms.

Policy Iteration

Now the policy-based, model-based quadrant. Unlike value iteration, here we separate policy evaluation from policy improvement:

1. Policy evaluation: solve

\(V^{\pi}(s) = \mathbb{E}_{s’}\big[R(s,\pi(s),s’) + \gamma V^{\pi}(s’)\big]\)

Unlike value iteration, this is a linear system of equations that you can invert directly, since π is known.

2. Policy improvement: set

\( \pi’(s) = \arg\max_a \mathbb{E}_{s’}\big[R(s,a,s’) + \gamma V^{\pi}(s’)\big]\)

And repeat until convergence.

Proof of Convergence

The first step is showing that V(s) can only increase for any given s.

Define T^π as the “Bellman expectation operator,” which updates a state-value function V in the “direction of” π:

\((T^\pi V)(s) = \mathbb{E}_{s’}[R(s,\pi(s),s’) + \gamma V(s’)]\)

(Note that V might not have been generated by following π.) By definition, V^π = T^π V^π. Notice that if you apply T^π’ enough times to any value function V, you’ll end up with V^π’. If π’ is greedy w.r.t. V^π, then

\(V^\pi \le T^{\pi’}V^\pi \le (T^{\pi’})^2 V^\pi \le \dots \to V^{\pi’}.\)

since after enough iterations of T^π’, the policy becomes π’. The first inequality holds because we are using the same state-values, and only deviating if the new action leads to a strictly higher state-value. The second inequality is more subtle, but it relies on the monotonicity of the Bellman update operator. If you have two value functions where V(s) > U(s), then T^πV(s) > T^πU(s). This result comes directly from the Bellman operator definition if you compare each term of the expression. We’re just applying this property to the last two terms of the inequality to produce the next term, infinitely many times.

So each greedy improvement can only increase value. Since there are finitely many deterministic policies (|A|^|S|), this process must terminate eventually.

Model-Free Value Iteration (Q-Learning)

In the real world, we might not know P and R. We just have to start taking actions and figuring it out empirically. This leads us to the “model-free” methods. We can’t directly compute the fixed point from before, because it relies on knowing P and the true reward function R:

\(V^{*}(s) = \max_a \sum_{s’} P(s’ \mid s,a) * \big(R(s,a,s’) + \gamma V^{*}(s’)\big)\)

So instead we define a new fixed point, which relies on a value function for each state-action pair:

\(Q^*(s,a) = \mathbb{E}[R(s,a,s’)] + \gamma \mathbb{E}[\max_{a’} Q^*(s’,a’)]\)

In other words, the value of a state-action pair is the expected reward, plus the discounted value of the next state-action pair you’d find yourself in.

Naively you might try approximating this by gathering observations:

\(Q(s,a) \leftarrow r + \gamma \max_{a’} Q(s’,a’)\)

But that doesn’t quite work. r is noisy - it varies based on which s’ you land in. You need an averaging scheme. The natural instinct might be to use a sample mean:

\(Q(s,a) \leftarrow \tfrac{1}{t+1}[r+\gamma\max_{a’}Q(s’,a’)] + \tfrac{t}{t+1}Q(s,a)\)

This works, but exploration is non-stationary. Q itself is changing, so early samples are inaccurate. Instead, we use an exponential moving average (EMA):

\(Q(s,a) \leftarrow \alpha[r+\gamma\max_{a’}Q(s’,a’)] + (1-\alpha)Q(s,a)\)

Iterate, slowly lower alpha, and the process converges. Each update adds another discounted term, just like value iteration.

Proof of Convergence

This is trickier than proving convergence for the model-based methods, because now it’s stochastic. The standard proof defines each update as:

\(Q_{t+1}(s_t,a_t)-Q_t(s_t,a_t) = \alpha [TQ_t + M_{t+1} - Q_t(s_t,a_t)]\)

where M is zero-mean noise. Ignoring noise, this looks like:

\(\frac{Q_{t+1}-Q_t}{\alpha} = TQ_t - Q_t\)

Then they define a continuous version of Q called q, which is respect to a new variable tau:

\(\tau=\sum\alpha\)

In the limit as alpha goes to 0,

\(\frac{dq}{d\tau} = Tq - q\)

This ODE is used to demonstrate convergence. The full analysis is beyond the scope of this post.

Model-Free Policy Iteration

Now let’s try to apply the same methodology to policy iteration, just as Q-learning stochastically approximated value iteration.

In principle, we could evaluate Q^π by sampling, then improve π, and repeat. But exact evaluation by sampling is very slow and requires waiting for convergence each round. Worse, unlike the model-based case, you can’t invert the system of equations for V^π. So the advantages of policy iteration vanish in the model-free setting.

A practical compromise is approximate policy iteration: run only k evaluation steps before improving the policy. This weakens convergence guarantees. With k=1, you get a popular method called SARSA.

SARSA’s policy is to follow Q most of the time, except for epsilon probability where you take a random action, called an “epsilon-greedy policy”:

\(\pi(a \mid s) = \begin{cases} 1 - \varepsilon + \dfrac{\varepsilon}{|A|}, & a = \arg\max_{a'} Q(s, a') \\[6pt] \dfrac{\varepsilon}{|A|}, & \text{otherwise.} \end{cases}\)

We update with:

\(Q(s_t,a_t) \leftarrow (1-\alpha)Q(s_t,a_t) + \alpha\big[r(s_t,a_t,s_{t+1}) + \gamma Q(s_{t+1},a_{t+1})\big]\)

This is called “TD(0)”, or temporal-difference learning with lambda equals 0. Temporal-difference learning allows us to extend further. Instead of just one-step lookahead, you can mix multiple n-step returns G_n:

\(G_t^{(\lambda)} = (1-\lambda)\sum_{n=1}^\infty \lambda^{n-1} G_n\)

In practice, computing this infinite sum is approximated dynamically. Lots of simple algebra goes into deriving the recursion (eligibility traces), but I’ll skip it here.

Wrap-Up

This is why you don’t really see a neat “model-free policy iteration.” Without P and R, exact evaluation is gone, and requiring near-converged sample evaluation before every improvement is prohibitively inefficient.

Is that all we need to know for reinforcement learning? Unfortunately the methods above don’t work in many domains. They require not “too big” of a state-action table, and there’s no way to handle continuous action spaces. I’ll cover how you can solve these more complex scenarios in my next post.

For a comprehensive overview that overlaps CS 188 material and this post, see Lilian Weng’s excellent writeup.